Logistic Regression Algorithm in Practice

Introduction

Logistic regression is a statistical model which is extensively used in binary classification tasks. The name logistic because it uses a logistic function to do the classification. The logistic function is also known as cross-entropy. Besides this, we use a special function known as sigmoid function to prevent the impact of outliers in the whole modeling.

Credits of Cover Image - Photo by Luis Soto on Unsplash

Mathematical Model

Given the data points, we need to classify them into two classes (binary classification). We shall find a separating hyperplane to divide the classes.

$$f(w, b) = w^Tx+ b \rightarrow (1)$$

The notation of sigmoid function can be stated as -

$$S(x) = \frac{1}{1 + e^{-x}}$$

The plot of the sigmoid function is -

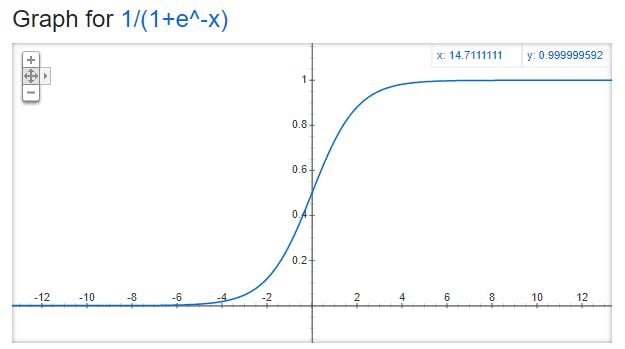
Credits - The above plot is taken from Google.

If we observe the bounds of the curve, the upper bound is 1 and the lower bound is 0. The sigmoid function only returns the value in the range of 0 and 1 which is sufficient for doing binary classification.

If we use a sigmoid function by substituting the above approximation (1), we get -

$$\implies \frac{1}{1 + e^{-(w^Tx + b)}} \rightarrow (2)$$

Equation (2) is the actual model which is used in predicting the class label.

Given x, w, and b. We need to pass this in the model that in turn returns a probability value.

If the probability value is less than 0.5, the value is predicted as 0.
If the probability value is greater than equal to 0.5, the value is predicted as 1.

Everything is properly written except two things which are still unknown. The two things are the parameters w and b. The error in the model depends on these two parameter values. Here, w is the coefficient and b is the intercept. We cannot simply assign random values for w and b. Instead, they are to be chosen wisely with the help of the stochastic gradient descent process.

Stochastic Gradient Descent (SGD)

The ultimate goal is now to find the best values for w and b. Here w is a vector and b is a scalar value. We shall use the logistic function or cross-entropy function to find these values.

It is stated as -

$$L = \frac{1}{n} \sum_{i=1}^n \bigg[-y_i \log\big[\sigma(w^Tx_i + b)\big] - (1 - y_i) \log\big[1 - \sigma(w^Tx_i + b)\big]\bigg] \rightarrow (3)$$

Note - Sigmoid function is often denoted as sigma.

SGD is an iterative process where we initially assign random values (possibly 0) for both w and b. At every iteration,

For w, we differentiate (3) with respect to w and obtain dw.
For b, we differentiate (3) with respect to b and obtain db.

Mathematically, it can be represented as -

$$dw = \frac{1}{n} \sum_{i=1}^n x_i \big[\sigma(w^Tx_i + b) - y_i\big]$$

and

$$db = \frac{1}{n} \sum_{i=1}^n \big[\sigma(w^Tx_i + b) - y_i\big]$$

Note - I have actually differentiated the above on a paper and verified.

We update/replace the actual w and b with dw and db respectively at every iteration until the values are not fully minimized. The updating process can be understood in the following way.

$$w = w - \alpha * dw$$

and

$$b = b - \alpha * db$$

Now that we have understood the complete process, let's implement the same from scratch.

Logistic Regression - Code

We will start by importing the necessary libraries as always at the start.

Libraries

import warnings
warnings.filterwarnings('ignore')

import numpy as np
import pandas as pd

from matplotlib import pyplot as plt
from sklearn.datasets import make_classification

Data Creation

For now, we will depend on a toy dataset that we can easily create by the module sklearn.

X, y = make_classification(
    n_samples=500, 
    n_features=2, 
    n_informative=2,
    n_redundant=0,
    n_clusters_per_class=1,
    n_classes=2,
    random_state=60
)
d = {'col{}'.format(i + 1) : X[:,i] for i in range(len(X[0]))}
df = pd.DataFrame(d)
df['label'] = y

Data Splitter

We need to split the data into two - the training set and the testing set. We do this by a random splitter function.

def splitter(dframe, percentage=0.8, random_state=True):
    """
    :param DataFrame dframe: Pandas DataFrame
    :param float percentage: Percentage value to split the data
    :param boolean random_state: True/False
    :return: train_df, test_df
    """
    if random_state:
        dframe = dframe.sample(frac=1)

    thresh = round(len(dframe) * percentage)
    train_df = dframe.iloc[:thresh]
    test_df = dframe.iloc[thresh:]

    return train_df, test_df

Train Test Split

train_df, test_df = splitter(dframe=df)

Construction

class LogisticRegression():

The name of the classifier is LogisticRegression and it is a class where we define other methods.

`init()` Method

    def __init__(self, train_df, test_df, label, lambda_=0.0001, n_iters=1000):
        self.lambda_ = lambda_
        self.n_iters = n_iters

        self.X_train, self.y_train = self.split_features_targets(df=train_df, label=label)
        self.X_test, self.y_test = self.split_features_targets(df=test_df, label=label)
        self.X_train = self.X_train.values
        self.y_train = self.y_train.values
        self.X_test = self.X_test.values
        self.y_test = self.y_test.values
        self.n_ = len(self.X_train)

        self.w, self.b = self.find_best_params()

The above method is a constructor that takes five parameters -

train_df → refers to the subset of the data that is used to train the regressor.
test_df → refers to the subset of the data that is used to test the regressor.
label → refers to the series of data which is actually the column name of the class label.
lambda_ → refers to a constant that is used to update the parameters during the process of SGD.
n_iters → refers to a constant that is used to decide the total iterations of the process of SGD.

`split_features_targets()` Method

    def split_features_targets(self, df, label):
        X = df.drop(columns=[label], axis=1)
        y = df[label]
        return X, y

The above method is used to separate features and targets from the data. It takes two parameters -

df → refers to the entire dataset that is passed for classifying.
label → refers to the series of df which is actually the column name of the class label.

`sigmoid()` Method

    def sigmoid(self, z):
        return 1 / (1 + np.exp(-z))

The above method is a sigmoid function that takes one parameter. It is used to return the value in the range of 0 and 1.

z → refers to a data value.

`diff_params_wb()` Method

    def diff_params_wb(self, w, b):
        lm = np.dot(self.X_train, w) + b
        z = self.sigmoid(z=lm)
        w_ = (1 / self.n_) * np.dot((z - self.y_train), self.X_train)
        b_ = (1 / self.n_) * np.sum((z - self.y_train))
        return w_, b_

The above method is used to differentiate the parameters. It takes two functional parameters -

w → refers to the initial weight vector that is used in the process of SGD.
b → refers to the initial intercept value that is used in the process of SGD.

`find_best_params()` Method

    def find_best_params(self):
        ow = np.zeros_like(a=self.X_train[0])
        ob = 0

        for i in range(self.n_iters):
            w_, b_ = self.diff_params_wb(w=ow, b=ob)
            ow = ow - (self.lambda_ * w_)
            ob = ob - (self.lambda_ * b_)

        return ow, ob

The above method is used to get the best (minimal) values of the parameters w and b. It takes no functional parameters. This method follows the process of SGD to update the original values of w and b iteratively.

`draw_line()` Method

    def draw_line(self, ax):
        if (len(self.w) == 2):
            a, b = self.w
            c = self.b

            y_min = np.min(self.X_train)
            y_max = np.max(self.X_train)

            p1 = [((-b*y_min - c)/a), y_min]
            p2 = [((-b*y_max - c)/a), y_max]

            points = np.array([p1, p2])
            ax.plot(points[:, 0], points[:, 1], color='#BA4A00')
        return None

The above method is used to draw a hyperplane. It takes one parameter -

ax → refers to the axis for which the hyperplane is plotted.

`predict()` Method

    def predict(self, with_plot=False):        
        y_test_preds = self.sigmoid(z=(np.dot(self.X_test, self.w) + self.b))
        y_test_preds_c = np.where((y_test_preds >= 0.5), 1, 0)
        y_train_preds = self.sigmoid(z=(np.dot(self.X_train, self.w) + self.b))
        y_train_preds_c = np.where((y_train_preds >= 0.5), 1, 0)

        if with_plot:
            fig = plt.figure(figsize=(10, 4))

            ax1 = fig.add_subplot(1, 2, 1)
            ax1.title.set_text('Training')
            ax1.scatter(self.X_train[:, 0], self.X_train[:, 1], c=y_train_preds_c, label='points')
            self.draw_line(ax=ax1)
            ax1.legend()

            ax2 = fig.add_subplot(1, 2, 2)
            ax2.title.set_text("Testing")
            ax2.scatter(self.X_test[:, 0], self.X_test[:, 1], c=y_test_preds_c, label='points')
            self.draw_line(ax=ax2)
            ax2.legend()

            plt.show()
        return y_test_preds_c

The above method is used to predict the class label for the new unseen data. It takes one parameter (which is optional) -

with_plot → refers to a boolean value to decide if to plot the best fit line along with the data points.

By default, this function parameter takes the False value and therefore optional.

`score()` Method

    def score(self, preds):
        preds = np.array(preds)
        if (len(self.y_test) == len(preds)):
            non_z = np.count_nonzero(a=np.where((preds == self.y_test), 1, 0))
            return non_z / len(preds)
        return "Lengths do not match"

The above method is used to compute the level of accuracy score that determines whether a model is performing well or not. It is a fraction of the total number of correctly classified data with the total number of all the data points. Generally, the model whose accuracy level is greater than 0.80 or 80 is considered to be a good model. It takes two parameters -

preds → refers to an array of predictions (class labels).

Full Code

class LogisticRegression():
    def __init__(self, train_df, test_df, label, lambda_=0.0001, n_iters=1000):
        self.lambda_ = lambda_
        self.n_iters = n_iters

        self.X_train, self.y_train = self.split_features_targets(df=train_df, label=label)
        self.X_test, self.y_test = self.split_features_targets(df=test_df, label=label)
        self.X_train = self.X_train.values
        self.y_train = self.y_train.values
        self.X_test = self.X_test.values
        self.y_test = self.y_test.values
        self.n_ = len(self.X_train)

        self.w, self.b = self.find_best_params()

    def split_features_targets(self, df, label):
        X = df.drop(columns=[label], axis=1)
        y = df[label]
        return X, y

    def sigmoid(self, z):
        return 1 / (1 + np.exp(-z))

    def diff_params_wb(self, w, b):
        lm = np.dot(self.X_train, w) + b
        z = self.sigmoid(z=lm)
        w_ = (1 / self.n_) * np.dot((z - self.y_train), self.X_train)
        b_ = (1 / self.n_) * np.sum((z - self.y_train))
        return w_, b_

    def find_best_params(self):
        ow = np.zeros_like(a=self.X_train[0])
        ob = 0

        for i in range(self.n_iters):
            w_, b_ = self.diff_params_wb(w=ow, b=ob)
            ow = ow - (self.lambda_ * w_)
            ob = ob - (self.lambda_ * b_)

        return ow, ob

    def draw_line(self, ax):
        if (len(self.w) == 2):
            a, b = self.w
            c = self.b

            y_min = np.min(self.X_train)
            y_max = np.max(self.X_train)

            p1 = [((-b*y_min - c)/a), y_min]
            p2 = [((-b*y_max - c)/a), y_max]

            points = np.array([p1, p2])
            ax.plot(points[:, 0], points[:, 1], color='#BA4A00')
        return None

    def predict(self, with_plot=False):        
        y_test_preds = self.sigmoid(z=(np.dot(self.X_test, self.w) + self.b))
        y_test_preds_c = np.where((y_test_preds >= 0.5), 1, 0)
        y_train_preds = self.sigmoid(z=(np.dot(self.X_train, self.w) + self.b))
        y_train_preds_c = np.where((y_train_preds >= 0.5), 1, 0)

        if with_plot:
            fig = plt.figure(figsize=(10, 4))

            ax1 = fig.add_subplot(1, 2, 1)
            ax1.title.set_text('Training')
            ax1.scatter(self.X_train[:, 0], self.X_train[:, 1], c=y_train_preds_c, label='points')
            self.draw_line(ax=ax1)
            ax1.legend()

            ax2 = fig.add_subplot(1, 2, 2)
            ax2.title.set_text("Testing")
            ax2.scatter(self.X_test[:, 0], self.X_test[:, 1], c=y_test_preds_c, label='points')
            self.draw_line(ax=ax2)
            ax2.legend()

            plt.show()
        return y_test_preds_c

    def score(self, preds):
        preds = np.array(preds)
        if (len(self.y_test) == len(preds)):
            non_z = np.count_nonzero(a=np.where((preds == self.y_test), 1, 0))
            return non_z / len(preds)
        return "Lengths do not match"

Logistic Regression - Testing

We have already created a toy data set. We just need to test the model on that data.

Note - The data that we created is random. Results may differ for each execution.

Object Creation

lr = LogisticRegression(
    train_df=train_df, 
    test_df=test_df, 
    label='label', 
    lambda_=0.001, 
    n_iters=100
)

Weights

print(lr.w)
# [-3.77376685e-02 -5.56964363e-06]

Intercept

print(lr.b)
# 0.0017126093242175264

Prediction

preds = lr.predict(with_plot=True)

Training & Testing Plot

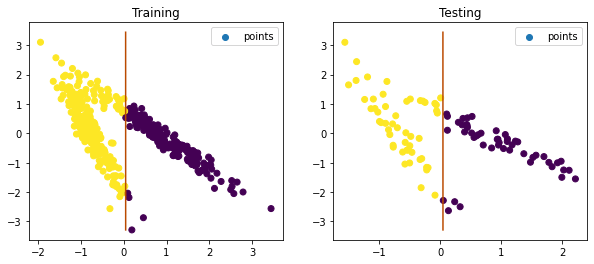
Performance Score

print(lr.score(preds=preds))
# 0.84

The accuracy happens to be >= 84% which is a decent percentage and hence the model is good.

Challenges

Well, this entire code is been developed from scratch and it is sure that it, by performance - may not be as efficient as the library methods. But, it was good to understand the mathematics behind the work.

My code is slow.
In this article, we considered linearly separable data. In the case of non-linearly separable data, we need to do feature transformation.
No regularization is implemented.
Although outliers do not impact much because of the sigmoid function that is been used. But still, we can remove them to avoid problems.
In real life, the data will not be like toy data set. It will be completely different and challenging also.

References

YouTube video → bit.ly/2UDmtZM
Wikipedia article → en.wikipedia.org/wiki/Logistic_regression

End

Logistic Regression Algorithm in Practice

What the logistic regression algorithm is and how it is used in regression tasks.

Table of contents

Introduction

Mathematical Model

Stochastic Gradient Descent (SGD)

Logistic Regression - Code

Libraries

Data Creation

Data Splitter

Construction

`init()` Method

`split_features_targets()` Method

`sigmoid()` Method

`diff_params_wb()` Method

`find_best_params()` Method

`draw_line()` Method

`predict()` Method

`score()` Method

Logistic Regression - Testing

Object Creation

Weights

Intercept

Prediction

Performance Score

Challenges

References

Logistic Regression Algorithm in Practice

What the logistic regression algorithm is and how it is used in regression tasks.

Table of contents

Introduction

Mathematical Model

Stochastic Gradient Descent (SGD)

Logistic Regression - Code

Libraries

Data Creation

Data Splitter

Construction

__init__() Method

split_features_targets() Method

sigmoid() Method

diff_params_wb() Method

find_best_params() Method

draw_line() Method

predict() Method

score() Method

Logistic Regression - Testing

Object Creation

Weights

Intercept

Prediction

Performance Score

Challenges

References

`init()` Method

`split_features_targets()` Method

`sigmoid()` Method

`diff_params_wb()` Method

`find_best_params()` Method

`draw_line()` Method

`predict()` Method

`score()` Method