Table of contents
Introduction
The word intersection in mathematics is termed as the similar (smaller) objects between two different objects. Intuitively, we can say the intersection of objects is that it belongs to all of them.
Credits of Cover Image - Photo by Benjamin Elliott on Unsplash
Geometrically speaking, if we have two distinct lines (assuming these lines are two objects), the intersection of these two lines would be the point where both the lines meet. Well, in the case of parallel lines, the intersection doesn’t exist. Geographically, the common junction between two or more roads can be taken as the area or region of intersection.
In Set theory, the intersection of two objects such as A and B is defined as the set of elements contained in both A and B. Symbolically, we represent the intersection as -
We also the above symbol as AND. Programatically this becomes very easy to code or to find the intersection between two sets.
Using NumPy, we can find the intersection of two matrices in two different ways. In fact, there are in-built methods with which we can easily find.
Let’s first define the two matrices of the same size.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>>
>>> a = np.random.randint(low=0, high=2, size=(5, 5))
>>> b = np.random.randint(low=0, high=2, size=(5, 5))
>>>
>>> print(a)
[[1 0 1 1 0]
[1 0 0 1 0]
[1 0 1 1 0]
[1 0 1 0 1]
[0 1 0 0 0]]
>>>
>>> print(b)
[[0 0 1 1 0]
[0 0 0 0 0]
[1 0 0 1 1]
[0 0 1 1 0]
[0 1 0 0 0]]
Using the operation &
In mathematics, intersection (&) is often called and. When we operate the same on a and b, using a broadcasting technique — automatically do the elementwise calculation.
>>> c = a & b
>>> print(c)
[[0 0 1 1 0]
[0 0 0 0 0]
[1 0 0 1 0]
[0 0 1 0 0]
[0 1 0 0 0]]
The result c is the intersection of the matrices a and b.
Using the method np.where()
To get the gist of np.where() — is a special method that acts like a ternary operator on NumPy arrays. By default, it takes 3 parameters -
condition→ The condition which is either true or false at certain positions (boolean value) of an array.x→ The value that gets replaced at the positions of the array where the condition is true.y→ The value that gets replaced at the positions of the array where the condition is false.
Let’s have a function to get the intersection of the matrices.
def intersect_matrices(mat1, mat2):
if not (mat1.shape == mat2.shape):
return False
mat_intersect = np.where((mat1 == mat2), mat1, 0)
return mat_intersect
If we call the above function with our matrices a and b, we get -
>>> c = intersect_matrices(mat1=a, mat2=b)
>>> print(c)
[[0 0 1 1 0]
[0 0 0 0 0]
[1 0 0 1 0]
[0 0 1 0 0]
[0 1 0 0 0]]
If we visualize the above results, we can get -
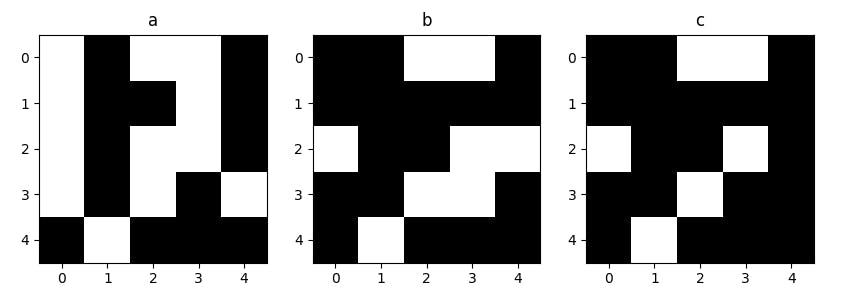
In the plot, white patches represent the true values and black patches represent the false values. Particularly, in subplot c, white patches represent the intersection value of sets a, and b.
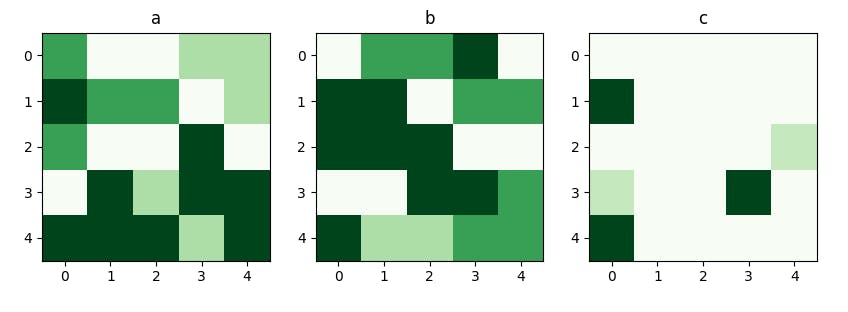
Note: The above implementation is done for the matrices which are of binary format. When we have values other than 0 and 1. It is better to go with the second procedure where we replace the values with 0 at the positions where the condition is false.
For different values other than 0 and 1, we have the plot something like below.
End