Convert a Regular Matrix into Sparse Matrix in Python

Introduction

Matrix is a type of data structure similar to an array where values are stored in rows and columns. Here, the values are of a unique type. When dealing with matrices (linear algebra) in Machine Learning and NLP, we often hear about two types of matrices as -

• Dense Matrix - The matrix where most of the elements are non-zero. In this matrix, there are very few zero elements.

• Sparse Matrix - In contrast, the matrix where most of the elements zero and very few elements are non-zero.

Note - There are no criteria as such how many zero values in a matrix determine that there is a need to sparse the matrix.

Credits of Cover Image - Photo by Alexander Schimmeck on Unsplash

Algorithm Explanation

Imagine you have a large matrix with N rows and M columns in which most of the values are zeros. You are asked to consider only non-zero elements since zero elements do not add much value. Definitely, you have time and space constraints since you are dealing with a very large matrix.

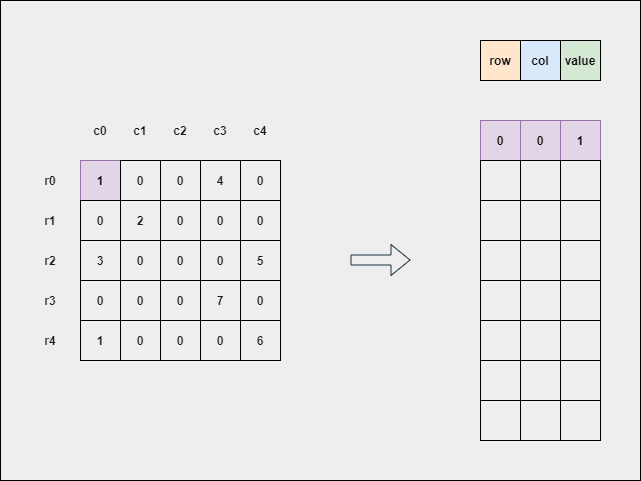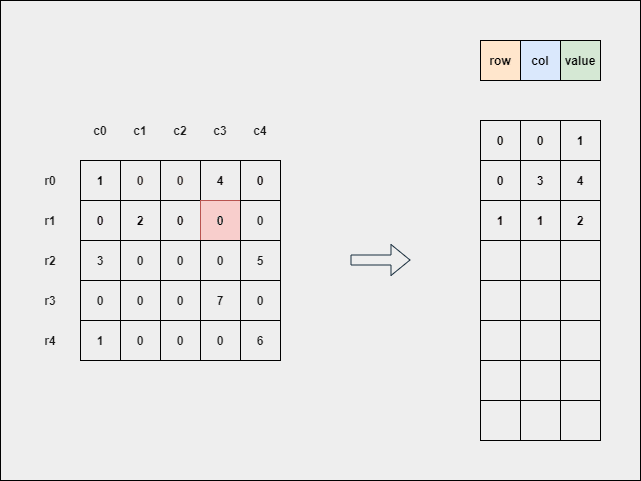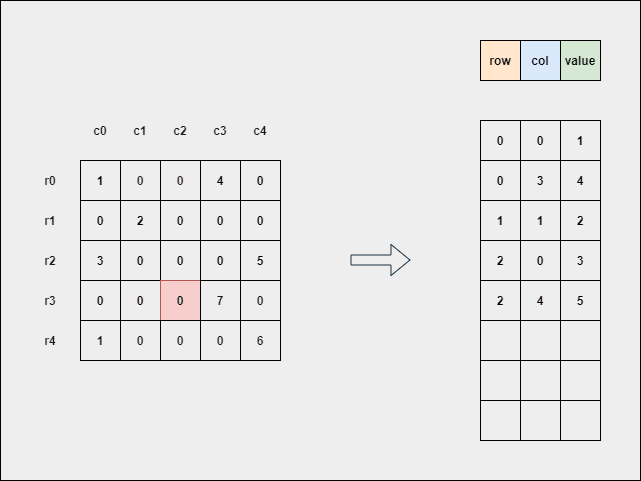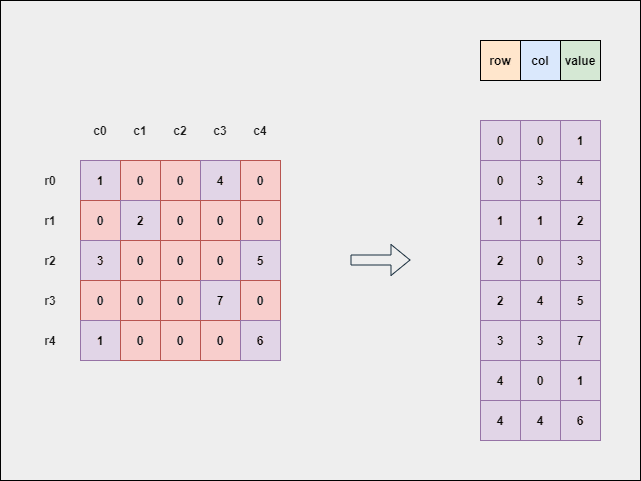
The simple method here is to neglect all 0's and store the non-zero elements in the form of [ row_index, col_index, non-zero_value ].

Approach:

1. Iterate through each row of an input matrix.
2. Iterate through each value of each row.
3. If (value == 0) → skip.
4. If (value != 0) → obtain the row number and column number along with the value from the input matrix.
5. Save the result as [ row, column, value ] for every row and column.
6. Stop.

Visual Explanation

Let's say we are given a matrix that has most of the elements to be 0.

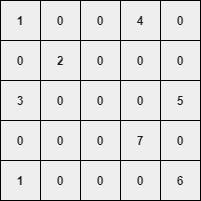
The following GIF explains how to obtain the sparse matrix (GIF by Author).

Time to Code

In this section, we will try to code this in two different ways. One, with the help of the scipy module and another, implementing our own sparse matrix.

Let's get started ...

Necessary Imports

import numpy as np
from scipy.sparse import csr_matrix

Random Matrix Creation

Just for the demonstration, we will make sure that the matrix contains 0 elements the most.

>>> mat = np.random.randint(low=0, high=3, size=(5, 5))
>>> print(mat)
[[2 2 0 2 0]
 [2 1 0 0 2]
 [2 1 0 1 0]
 [0 1 2 0 2]
 [0 1 2 2 1]]

SCIPY Implementation

With the help of the method csr_matrix() we can easily obtain the sparse matrix.

>>> smat = csr_matrix(mat)
>>> print(smat)
(0, 0)    2
(0, 1)    2
(0, 3)    2
(1, 0)    2
(1, 1)    1
(1, 4)    2
(2, 0)    2
(2, 1)    1
(2, 3)    1
(3, 1)    1
(3, 2)    2
(3, 4)    2
(4, 1)    1
(4, 2)    2
(4, 3)    2
(4, 4)    1

We can think of a dictionary in python which is a key and value paired. The above output is something like a dictionary where keys are the index location (row, column) and values are the actual non-zero elements.

Custom Implementation

In order to implement it from scratch, we can follow the Algorithmic approach that I have explained previously.

class SparseMatrix():
    def __init__(self, arr):
        self.arr = arr

    def retain_sparsity(self, to_dict=False):
        sparse_mat = [
            [rindx, cindx, val]
            for (rindx, row) in enumerate(self.arr)
            for (cindx, val) in enumerate(row)
            if (val != 0)
        ]

        if to_dict:
            sparse_mat = {(r, c) : v for (r, c, v) in sparse_mat}
        return sparse_mat

The above class SparseMatrix() has a method retain_sparsity wherein the default argument to_dict is False. The argument to_dict is used whether to get the output in the form of dictionary or not.

Object Creation

sparse = SparseMatrix(arr=mat)

Output - List

>>> smat_c = sparse.retain_sparsity()
>>> print(smat_c)
[[0, 0, 2],
 [0, 1, 2],
 [0, 3, 2],
 [1, 0, 2],
 [1, 1, 1],
 [1, 4, 2],
 [2, 0, 2],
 [2, 1, 1],
 [2, 3, 1],
 [3, 1, 1],
 [3, 2, 2],
 [3, 4, 2],
 [4, 1, 1],
 [4, 2, 2],
 [4, 3, 2],
 [4, 4, 1]]

Output - dictionary

>>> smat_d = sparse.retain_sparsity(to_dict=True)
>>> print(smat_d)
{(0, 0): 2,
 (0, 1): 2,
 (0, 3): 2,
 (1, 0): 2,
 (1, 1): 1,
 (1, 4): 2,
 (2, 0): 2,
 (2, 1): 1,
 (2, 3): 1,
 (3, 1): 1,
 (3, 2): 2,
 (3, 4): 2,
 (4, 1): 1,
 (4, 2): 2,
 (4, 3): 2,
 (4, 4): 1}

Conclusion

• When we have space constraints while working with large matrices, it is often preferred to convert the matrix into sparse representation and this really takes less space comparatively the original matrix.

• In fact, we can check the space (in bytes) occupied by the original matrix mat and the sparse matrix.

>>> from sys import getsizeof
>>> # checking the space of original matrix
>>> getsizeof(mat) 
156
>>> # checking the space of scipy sparse matrix
>>> getsizeof(smat)
24
>>> # checking the custom implementation sparse matrix
>>> getsizeof(smat_c)
92

• What we can observe is, the scipy method consumes less space than our custom method. It is because scipy is an optimized well-developed library mainly used for various scientific computations.

• It is always better to use library methods than our own code to achieve faster results with fewer space constraints.

---

Buy Me Coffee

If you have liked my article you can buy some coffee and support me here. That would motivate me to write and learn more about what I know.