#5 - Statistical Measures for Exploratory Data Analysis

Introduction

Statistics is a branch of mathematics (applied mathematics) concerned mainly with the analysis of the data. It includes - collection, analysis, interpretation, and presentation of huge numerical data. There are a variety of numerical measures such as mean, median, mode, percentiles, variance, and standard deviation to summarize the data.

We shall understand the meaning of each measure briefly and programmatically implement the same using Python.

Credits of Cover Image - Photo by Crissy Jarvis on Unsplash

Mean Computation

Mean is generally referred to as the average value for the given set of values. It is the central value or central tendency of a finite set of numbers (data). In a lot of ways, mean is misinterpreted as median (which is the middle value) but it more convenient to take mean as the measure of central tendency.

Formula

Let

$$X = [x_1, x_2, x_3, x_4, \dots, x_n]$$

be the finite set of numbers (data) and the mean of this data is given as

$$\mu = \frac{1}{n} \sum_{i=1}^n x_i$$

Code

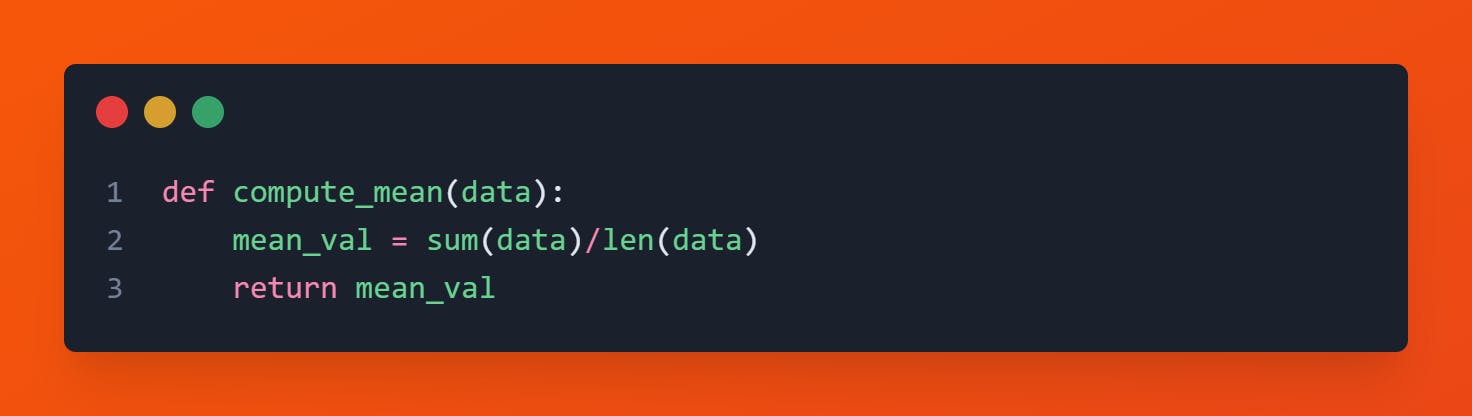
Limitation

• Means do get affected when introduced outliers in the data.

Median Computation

Median is generally referred to as the mid data point from the data provided. In other words, it is the value that separates the data into two - lower half and higher half. The only constraint to compute the median is that the data needs to be in sorted order.

Formula

Let

$$X = [x_1, x_2, x_3, x_4, \dots, x_n]$$

be the finite set of numbers (data) which is sorted and the median of the data is given as (considering the index starting from 0)-

• If n is odd, then

$$Med(X) = X\bigg[\frac{n}{2}\bigg]$$

• If n is even, then

$$Med(X) = \frac{(X[\frac{n}{2}-1] + X[\frac{n}{2}])}{2}$$

Code

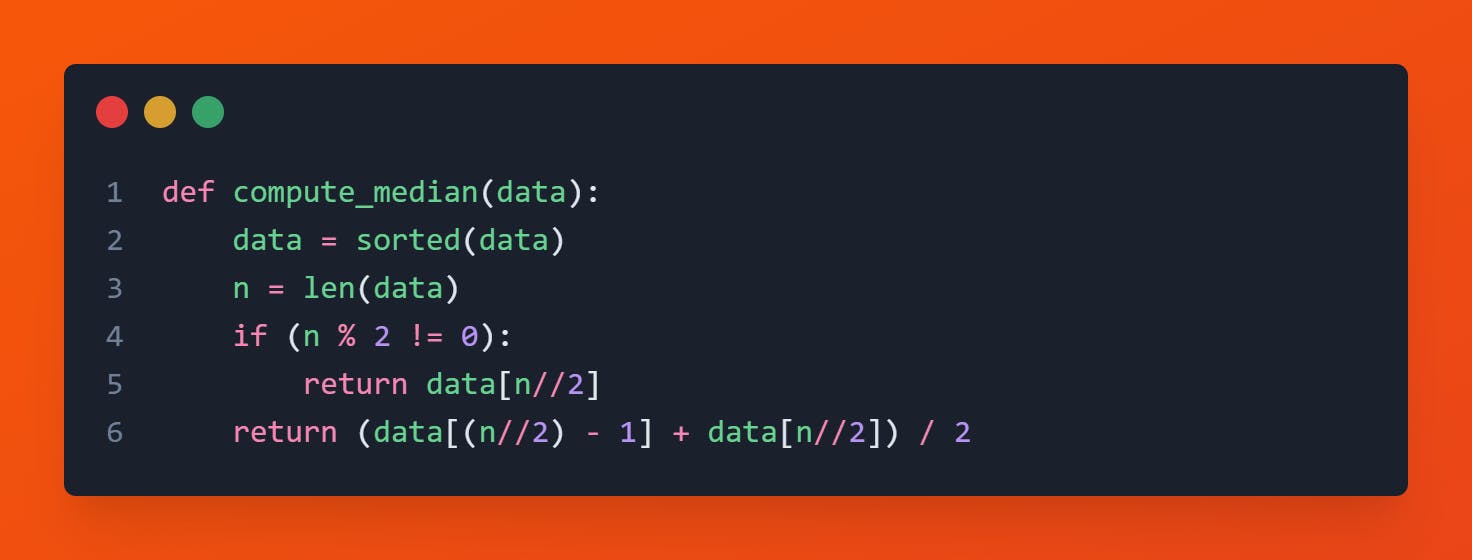
Pro

• Medians do not get affected when introduced outliers in the data.

Mode Computation

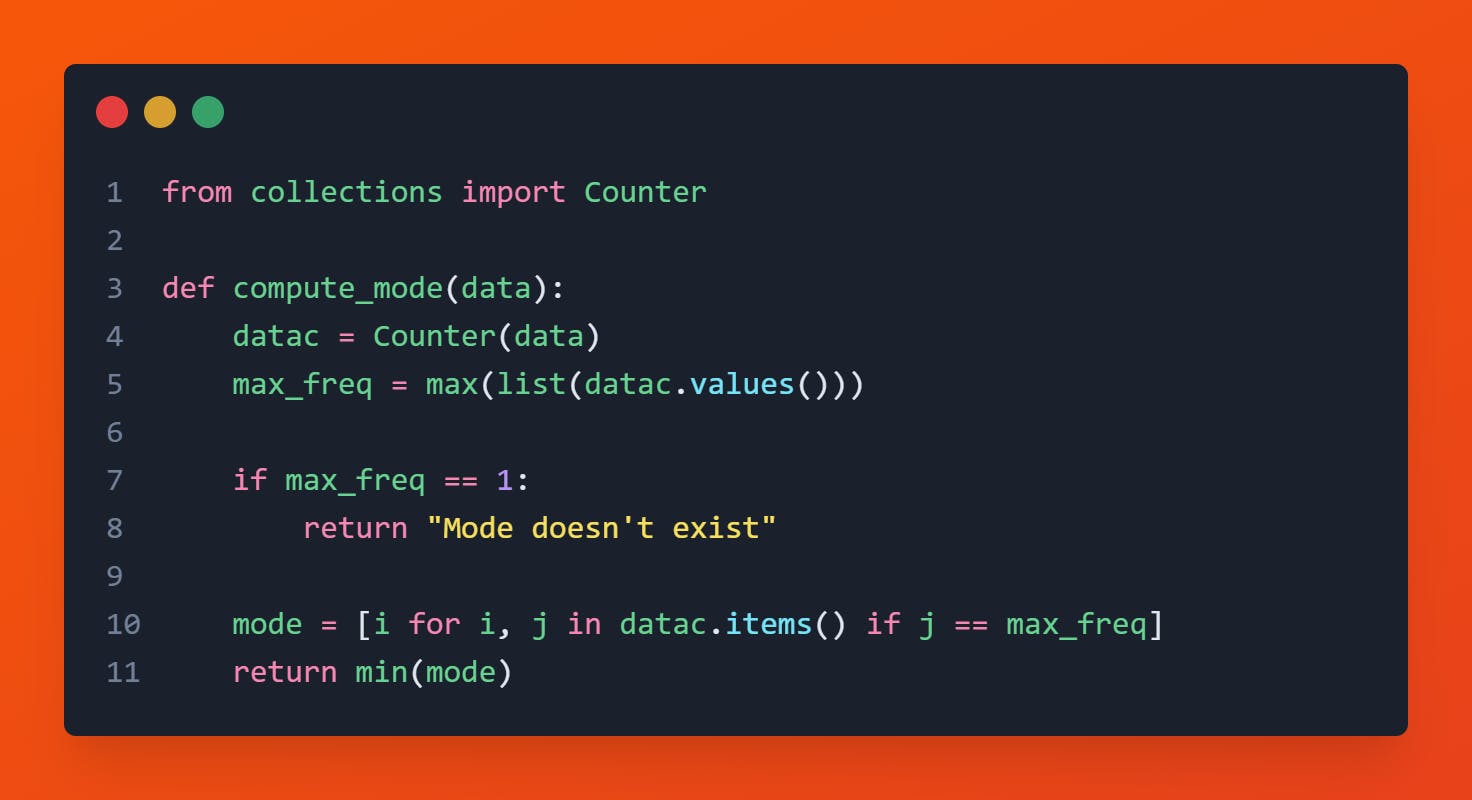
Mode is generally referred to as a number that appears most frequently in the given dataset. There is a formula to get the modal value which is more likely applicable to the data represented in class intervals. Other than that, we can easily compute the mode by counting the occurrence of each data point.

Code

Standard Deviation Computation

Standard Deviation is generally referred to as the overall dispersion of each data point with respect to the data mean. Here, dispersion is simply the distance that is measured. Always, the distances are positive, we never find the distance that is measured in negative. But, the dispersion for some points can be negative. In order to avoid that, we apply a mathematical hack that can be observed in the formula.

Formula

Let

$$X = [x_1, x_2, x_3, x_4, \dots, x_n]$$

be the finite set of numbers (data) and the standard deviation of the data is given as

$$\sigma = \sqrt{\frac{\sum_{i=1}^n (x_i - \mu)^2}{n}}$$

Code

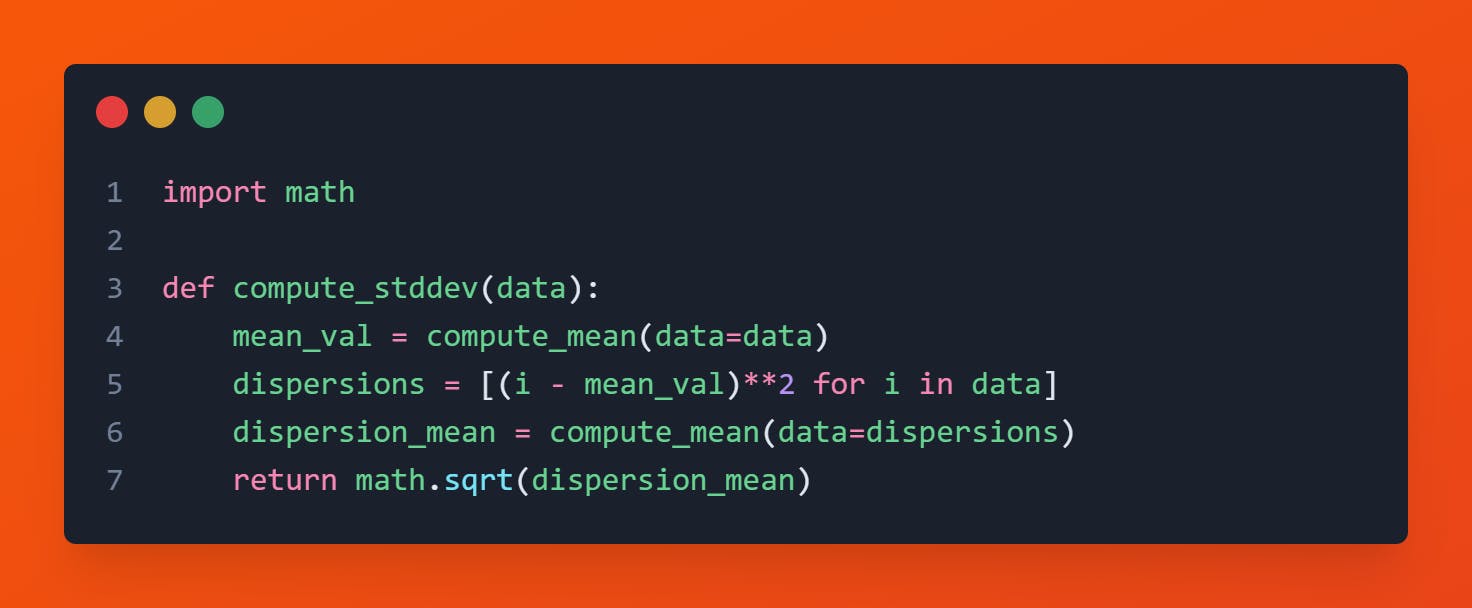
Limitation

• Standard Deviation does get affected when introduced outliers in the data.

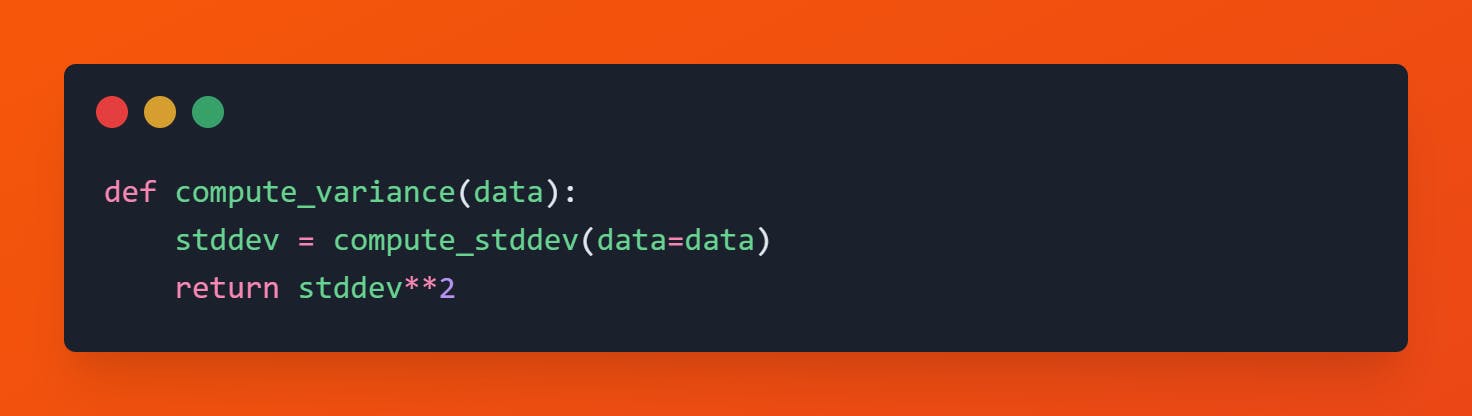
Variance Computation

Variance is generally referred to as the square of standard deviation. In case if the data is normally distributed, then the standard deviation is equal to variance which is again equal to 1.

Formula

Let

$$X = [x_1, x_2, x_3, x_4, \dots, x_n]$$

be the finite set of numbers (data) and variance of the data is given as

$$Var(X) = \sigma^2$$

Code

Limitation

• Variance does get affected when introduced outliers in the data.

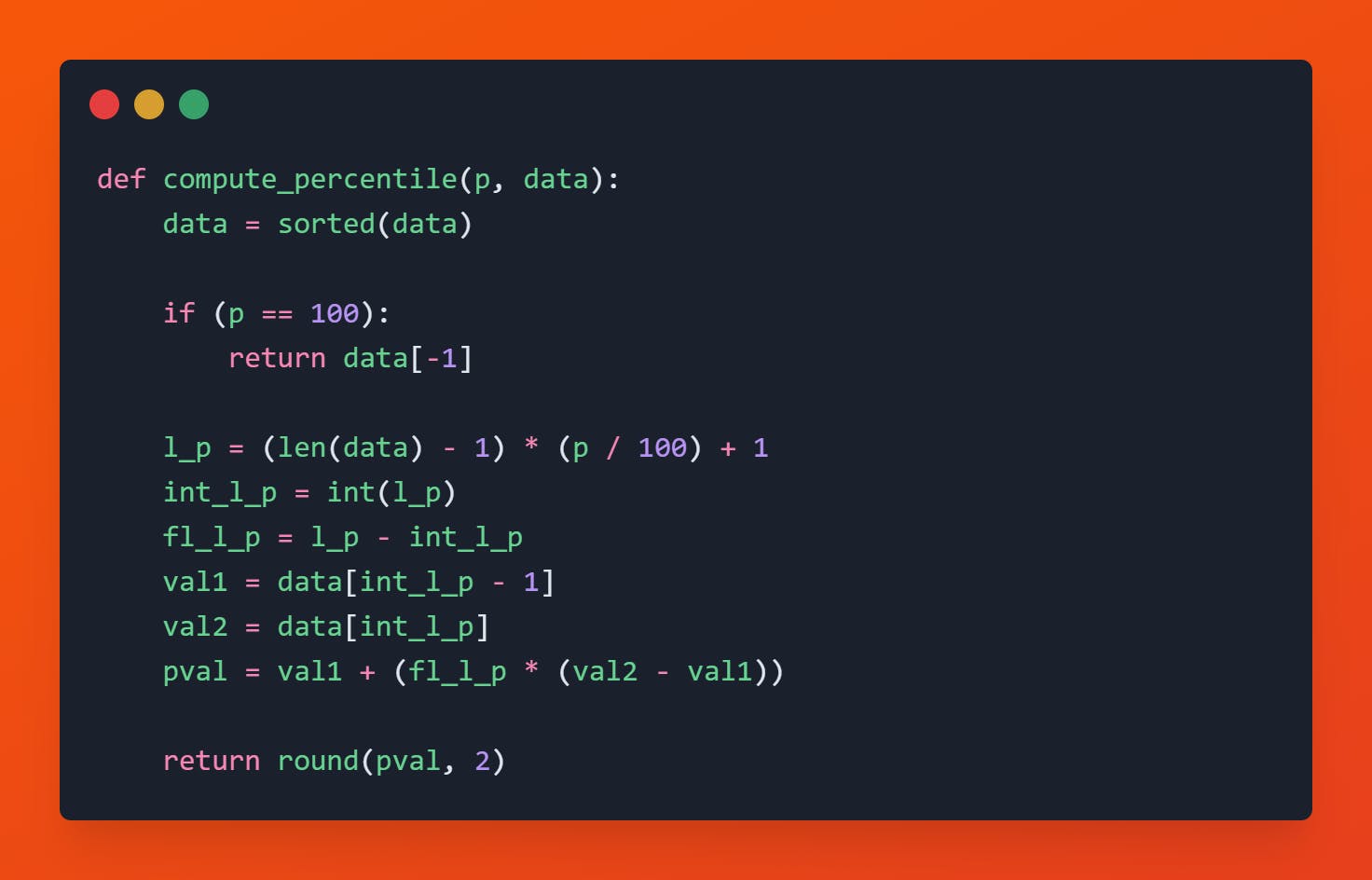
Percentile Computation

Percentile is generally referred to as the single score value which falls below the given percentage of score in its frequency distribution. The median value is also equal to the 50th percentile of the given data distribution.

Formula

Let

$$X = [x_1, x_2, x_3, x_4, \dots, x_n]$$

be the finite set of numbers (data) and location percentile can be computed by

$$l_p = \bigg[(n - 1) \frac{p}{100}\bigg] + 1$$

separate the integer part and floating part from the location percentile value and get the previous data value (integer part - 1) and current data value (integer part) with the help of indexing and compute the percentile value by

$$p_v = X[prev] + [\text{floating part of }l_p * (X[curr] - X[prev])]$$

Code

Limitation

• The data needs to in sorted order (ascending) to be able to compute percentile efficiently.

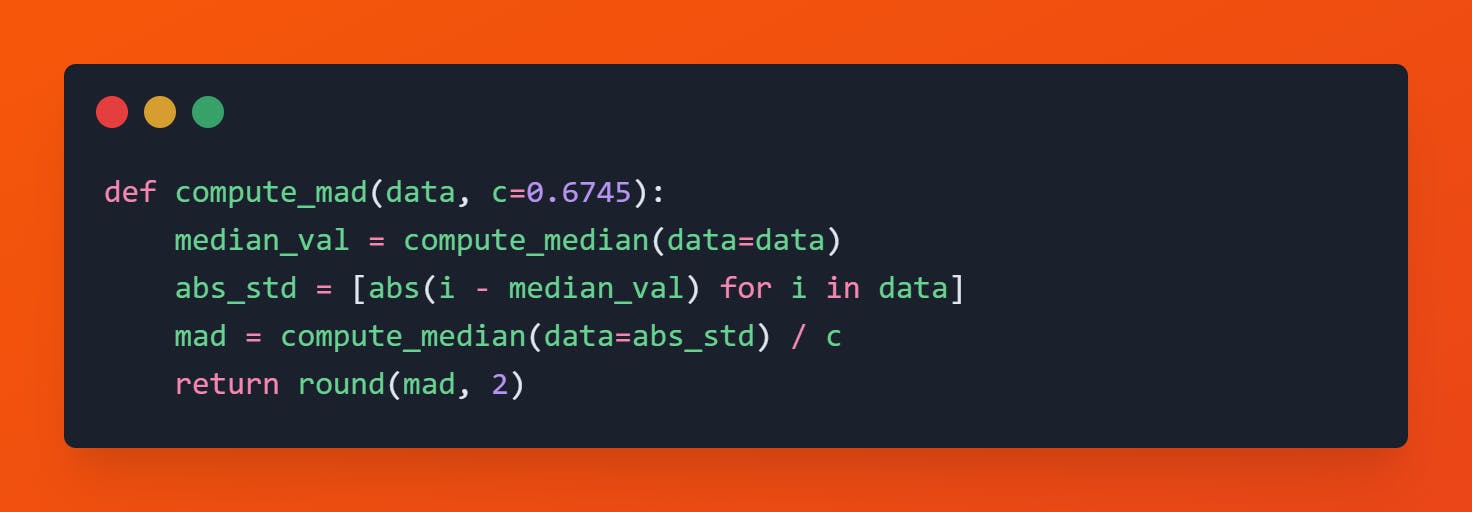
Median Absolute Deviation

Median Absolute Deviation is generally referred to as the median value of absolute dispersion from each data point to the median of the data itself. Standard deviation is computed with respect to the mean value whereas median absolute deviation (MAD) is computed with respect to the median value.

Formula

Let

$$X = [x_1, x_2, x_3, x_4, \dots, x_n]$$

be the finite set of numbers (data) and MAD of the data is given as

$$MAD(X) = Med(|x_i - Med(X)|)$$

Code

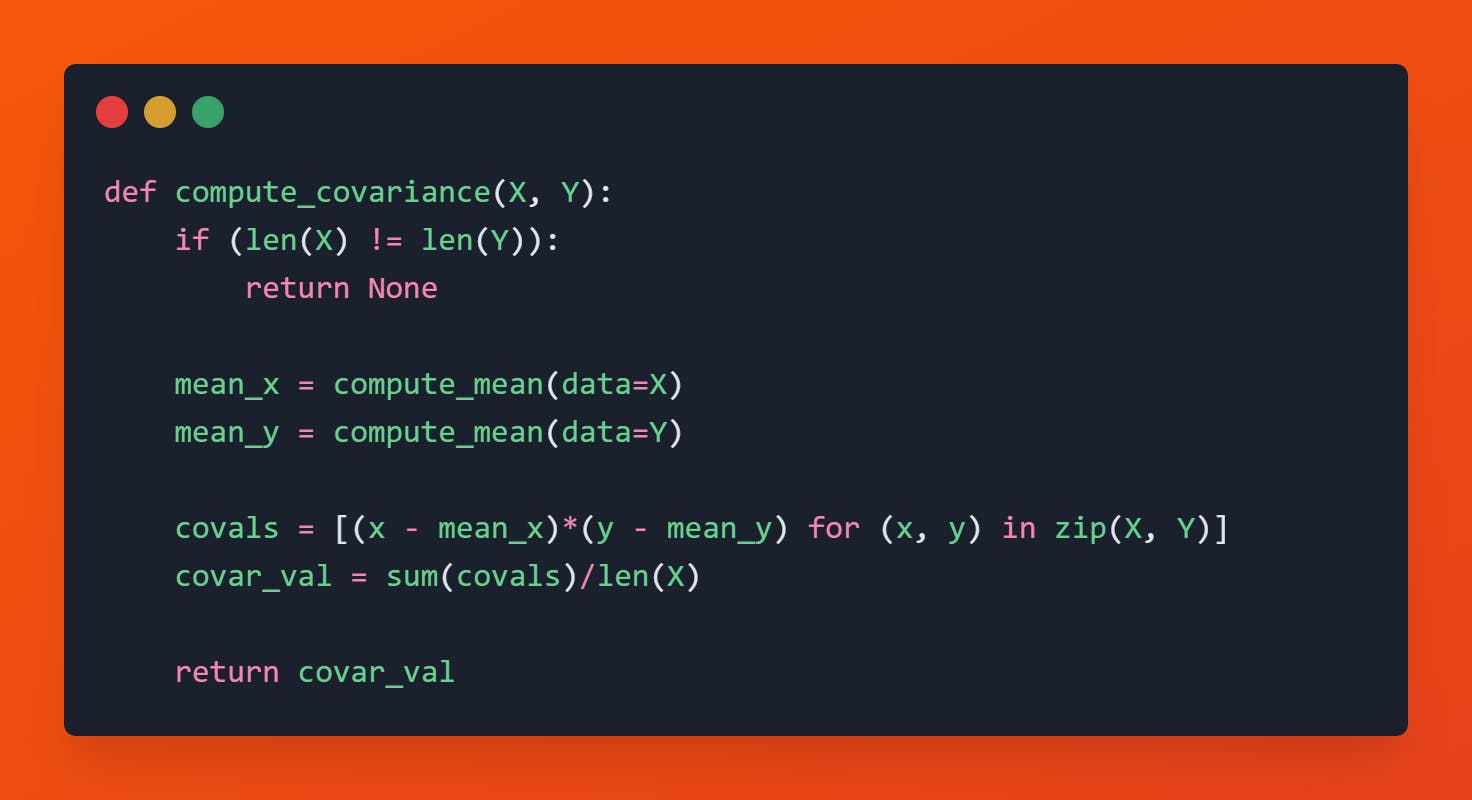
Covariance Computation

Covariance is generally referred to as a measure of the relationship between two random variables X and Y. This measure evaluates how much – to what extent – the variables change together. In other words, it is essentially a measure of the variance between two variables.

Formula

Let

$$X = [x_1, x_2, x_3, x_4, \dots, x_n]$$

and

$$Y = [y_1, y_2, y_3, y_4, \dots, y_n]$$

be two finite sets of numbers (data) and the Covariance of X and Y is given as

$$\text{Cov(X, Y)} = \frac{1}{n} \sum_{i=1}^n (x_i - \mu_x)(y_i - \mu_y)$$

Code

Types

• Positive Covariance → Indicates that two variables tend to move in the same direction.
• Negative Covariance → Indicates that two variables tend to move in the inverse direction.

Properties

• Cov(X, Y) = Cov(Y, X)
• Cov(X, X) = Var(X)

Correlation Computation

Correlation is generally referred to as a measure of the strength of the relationship between two finite sets (data). Correlation is the scaled measure of covariance. The correlation value is always in the range of -1 to +1.

Formula

Let

$$X = [x_1, x_2, x_3, x_4, \dots, x_n]$$

and

$$Y = [y_1, y_2, y_3, y_4, \dots, y_n]$$

be two finite sets of numbers (data) and the Correlation of X and Y is given as

$$\text{Corr(X, Y)} = \frac{\text{Cov(X, Y)}}{\sigma_X \sigma_Y}$$

Code

Types

• Positive Correlation → Indicates that two variables have a strong relationship and tend to move in a positive direction. The value is generally +1.
• Zero Correlation → Indicates that there is no relationship between two variables. The value is generally 0.
• Negative Correlation → Indicates that two variables have a strong relationship and tend to move in the inverse direction. The value is generally -1.

Full Code

import math
from collections import Counter

class StatsBasics():
    def compute_mean(self, data):
        mean_val = sum(data)/len(data)
        return mean_val

    def compute_median(self, data):
        data = sorted(data)
        n = len(data)
        mid_idx = n // 2

        if (n % 2 != 0):
            return data[mid_idx]
        return (data[mid_idx - 1] + data[mid_idx]) / 2

    def compute_mode(self, data):
        datac = Counter(data)
        max_freq = max(list(datac.values()))

        if (max_freq == 1):
            return "Mode doesn't exist"

        modals = [i for (i, j) in datac.items() if (j == max_freq)]
        return min(modals)

    def compute_stddev(self, data):
        mean_val = self.compute_mean(data=data)
        dispersions = [(i - mean_val)**2 for i in data]
        dispersion_mean = self.compute_mean(data=dispersions)
        return math.sqrt(dispersion_mean)

    def compute_variance(self, data):
        stddev = self.compute_stddev(data=data)
        return stddev**2

    def compute_percentile(self, p, data):
        data = sorted(data)

        if (p == 100):
            return data[-1]

        l_p = (len(data) - 1) * (p / 100) + 1
        int_l_p = int(l_p)
        fl_l_p = l_p - int_l_p
        val1 = data[int_l_p - 1]
        val2 = data[int_l_p]    
        pval = val1 + (fl_l_p * (val2 - val1))

        return round(pval, 2)

    def compute_mad(self, data, c=0.6745):
        median_val = self.compute_median(data=data)
        abs_std = [abs(i - median_val) for i in data]
        mad = self.compute_median(data=abs_std) / c
        return round(mad, 2)

    def compute_covariance(self, X, Y):
        if (len(X) != len(Y)):
            return None

        mean_x = self.compute_mean(data=X)
        mean_y = self.compute_mean(data=Y)

        covals = [(x - mean_x)*(y - mean_y) for (x, y) in zip(X, Y)]
        covar_val = self.compute_mean(data=covals)

        return covar_val

    def compute_correlation(self, X, Y):
        covar_val = self.compute_covariance(X=X, Y=Y)
        std_X = self.compute_stddev(data=X)
        std_Y = self.compute_stddev(data=Y)
        corr_val = covar_val / (std_X * std_Y)
        return corr_val

---

Well, that's all for now. This article is included in the series Exploratory Data Analysis, where I share tips and tutorials helpful to get started. We will learn step-by-step how to explore and analyze the data. As a pre-condition, knowing the fundamentals of programming would be helpful. The link to this series can be found here.